Auf der Ideallinie

Was es mit dem berühmten Anschneiden von Kurven auf sich hat

Kurven sind nun mal das wichtigste beim Motorradfahren. Doch wie fährt man sie richtig? Wo ist die berühmte Ideallinie? Was genau ist das eigentlich das berühmte Anschneiden von Kurven? Wie fährt man richtig in eine Kurve hinein, was macht man in der Kurve und wie fährt man wieder heraus?

Ein Auto lenkt man mit den Händen am Lenkrad, nämlich indem man es dreht, bis der richtige Lenkeinschlag für den jeweiligen Kurvenradius erreicht. Beim Motorrad ist das etwas anders. Auf den ersten Blick ist es ja ganz ähnlich wie beim Auto: Das Vorderrad lässt sich schwenken und das besorgt man mit dem Lenker. Also schlägt man ein und fährt dann seine Kurve?

„Where you look is where you ride“

Nur, wenn man ganz, ganz langsam fährt. Ab einer bestimmten Geschwindigkeit fährt das Motorrad, wenn man am linken Lenkerende zieht, nicht nach links sondern nach rechts. Und umgekehrt. Und überhaupt: Man lenkt ein Motorrad nicht wie ein Auto mit einem Lenkeinschlag, sondern mit den Augen und den zugehörigen Bewegungen des Kopfes und ggf. auch noch des Oberkörpers – und/oder mit Lenkimpulsen.

Es gibt da die ganz einfache Regel „Where you look is where you ride“. Wo du hin siehst, da fährst du auch hin. Deswegen muss man beim Motorradfahren auch immer auf die Straße schauen. Und zwar nicht direkt vor das Vorderrad, sondern ein ganzes Stück weiter nach vorne. Und dann fährt das Motorrad ganz von alleine dorthin, wo man hin will. Man muss sich lediglich angewöhnen, tatsächlich auch dahin zu gucken, wo man hin will. Und zwar in dem man den Kopf dorthin dreht oder noch besser: den Oberkörper.

Das komische ist, dass ich das – und meine Mopedkumpels vermutlich auch – all die vielen Kilometer, die wir als Teenager auf zwei Rädern zurückgelegten, nicht wussten. Auch in der Fahrschule für den Führerschein Klasse Eins hat uns das damals niemand gesagt. Vermutlich machten wir das intuitiv schon immer so.

Der Kurvenradius und die Hundekurve

Eine Kurve ist ein Kreisbogen. Nein, ist sie nicht. Jedenfalls nicht nur. Ich hab sie lediglich der Einfachheit halber in der Abbildung mit der Ideallinie weiter unten so gezeichnet. Tatsächlich kann man nicht schlagartig aus der Geraden in einen bestimmten Kurvenradius einbiegen. Würde man das tatsächlich schaffen, würde man dabei geradewegs von der Straße fliegen.

Zum Glück kann man das aber nicht. Dazu müsste man nämlich bei einem Auto zum Beispiel den Lenkeinschlag für den Kurvenradius in null Zeit herstellen. Beim Motorrad gibt es keinen Lenkeinschlag in dem Sinne, aber auch einen Übergang von der Geraden in einen Kurvenradius. Um das zu verstehen, braucht es ein wenig Physik. Aus der Sicht der Physik nämlich wird man in einer Kurve beschleunigt, auch wenn man sie mit absolut konstanter Geschwindigkeit durchfährt. Nach der Definition der Beschleunigung ist das Fahren auf einem Bogen nämlich nichts anderes als die Änderung einer Geschwindigkeit. Und Geschwindigkeit ist ein Vektor, denn sie hat immer außer einem Betrag (der auf dem Tacho steht) auch eine Richtung. Und wenn wir mit konstanter Geschwindigkeit – genauer müsste man sagen Bahngeschwindigkeit – um die Kurve fahren, ändert sich zwar nicht der Betrag des Geschwindigkeitsvektors aber seine Richtung. Und in der Kurve bewegen wir uns ja ständig in eine andere Richtung.

Zu einer Beschleunigung gehört immer eine Kraft. Und im Fall der Kurvenfahrt ist diese Kraft die Gegenkraft zur Fliehkraft, die der Grip unseres Reifens auf dem Asphalt aufbringen muss. Die Fliehkraft ist nämlich nichts anderes als unser Schwung in gerader Richtung, der uns tangential aus der Kurve fliegen lassen würde, wenn nicht der Grip des Reifens dagegenhalten würde. Die Kraft also, mit der unser Reifen uns auf der Straße hält, erzeugt die Beschleunigung, welche die kontinuierliche Änderung der Richtung unseres Geschwindigkeitsvektors darstellt.

Würden wir nun schlagartig von der geraden in einen bestimmten Kurvenradius übergehen – also wirklich tangential in eine Kurve einfahren – würde unsere Beschleunigung unendlich groß sein und damit auch die Kraft, die uns zur Kurvenaußenseite zieht. Aha! Jetzt wissen wir auch, was es mit den „abrupten Lenkbewegungen“ auf sich hat, die – besonders auf glattem Untergrund – „zu vermeiden“ sind: Wenn man beim Einfahren in eine Kurve den Radius zu schnell verkleinert, kann es eine so große Seitenkraft geben, dass wir aus derselbe fliegen, obwohl der Grip beim eigentlichen Radius, denn wir fahren wollte, ausgereicht hätte.

Tatsächlich wird das beim Bau von Straßen berücksichtigt. Deswegen sieht die Straße auf meiner Zeichnung auch etwas komisch aus, denn sie ist wie auch die Kurvenlinien der Einfachheit halber mit einem konstanten Radius und tangentialen Übergängen gezeichnet. Denn die Zeichnung soll uns nicht genau darstellen, wie wir in die Kurve hineinfahren, sondern lediglich verdeutlichen, welche unterschiedlichen Fahrlinien auf einer Kurve mit einem bestimmten Radius und einer bestimmten Fahrspurbreite möglich sind.

Das Einfahren in die Kurve mit einem sich langsam verkleinernden Radius und das Ausfahren aus der Kurve mit einem sich langsam vergrößernden Radius passiert von ganz alleine. Bei einer Autolenkung ist das sonnenklar: Man kann ja einen bestimmten Lenkeinschlag nicht in null Zeit herstellen und die Räder auch nicht in null zeit wieder gerade stellen. Beim Motorrad gibt es zwar keinen Lenkeinschlag, aber auch die Schräglage entsteht ja nicht schlagartig.

Das heißt selbst wenn eine Kurve in einer Straße tatsächlich mit einem konstanten Radius und tangentialem Ein- und Ausgang gebaut wäre, würden wir trotzdem zur Not richtig durchfahren können, nur käme es uns eventuell komisch vor, weil die Kurve der Straße nicht genau zu der Kurve passt, die wir fahren. Würde man aber ein Eisenbahngleis so bauen, würde der erste Zug, der in die Kurve fährt, sofort entgleisen. Das liegt daran, dass die Schienen tatsächlich versuchen würden, die Eisenbahnräder schlagartig in den Kurvenradius zu zwingen und das wurde eine – theoretisch – unendlich große Kraft zur Kurvenaußenseite erzeugen. Und praktisch wäre diese Kraft zwar nicht unendlich groß aber immerhin so groß, dass der Zug aus den Schienen springen würde. Deswegen geht es auf Schienen und auch auf der Straße immer mit Übergangsbögen in Kurven hinein.

Die mathematische Kurve, mit der man in eine Straßenkurve hinein fährt und die von Straßen- und Eisenbahnplanern an Kurven dran konstruiert wird, heißt Klothoide oder ganz ordinär Hundekurve und stellt eine Kurve dar, deren Radius sich ständig verkleinert. Man sagt auch, die Kurve zieht sich zu. Hundskurve heißt es deswegen, weil ein Hund beim Durchschwimmen eines strömenden Gewässers so eine Kurve beschreibt. Er peilt den Punkt am anderen Ufer an, zu dem er will und versucht dorthin zu gelangen.Weil ihn aber die Strömung abtreibt, muss er in einem immer steileren Winkel zum Ufer schwimmen, um schließlich doch noch dorthin zu gelangen wo er hin will.

Wie man in einer Kurve fahren kann: Nicht nur auf der Idealinie

Vom Wuffel im Fluss zurück zur Guffel auf der Straße. Stören wir uns nicht dran, dass die Zeichnung mit der Ideallinie in dieser Hinsicht ein wenig ungenau ist und richten wir unseren Blick aufs Wesentliche. Das Entscheidende nämlich ist, dass, egal ob es sich nun wirklich um einen einzigen tangential einsetzenden Kreisbogen handelt oder ob es am Anfang und am Ende Klothoiden als Übergangsbögen gibt, auf dem gleichen Fahrstreifen unterschiedlich große Kurvenradien möglich sind.

Und wir wollen einen möglichst großen Kurvenradius. Warum? Weil die Fliehkraft laut Physikstunde in goldenen Jugendtagen von dem Verhältnis unserer Bahngeschwindigkeit zum Kurvenradius abhängt. Bzw.von der Winkelgeschwindigkeit – was aber nix anderes ist. Je kleinerder Radius bei gleichen km/h auf der Uhr, desto größer die Fliehkraft. Oder: Je größer der Radius, desto flotter können wir müllern, ohne dass der Grip zum Abschied leise Servus sagt.

Die erste Möglichkeit wäre, wie sich das gehört in der Mitte des Fahrstreifens zu fahren. Das wäre dann die blaue Linie in der Zeichnung. Wir sehen im Bild, dass das bei einem Radius an der Mittellinie und einer 8 m breiten Straße bei der abgebildeten Kurve ein Radius von 10,3 m wäre. Das ist nun nicht viel.

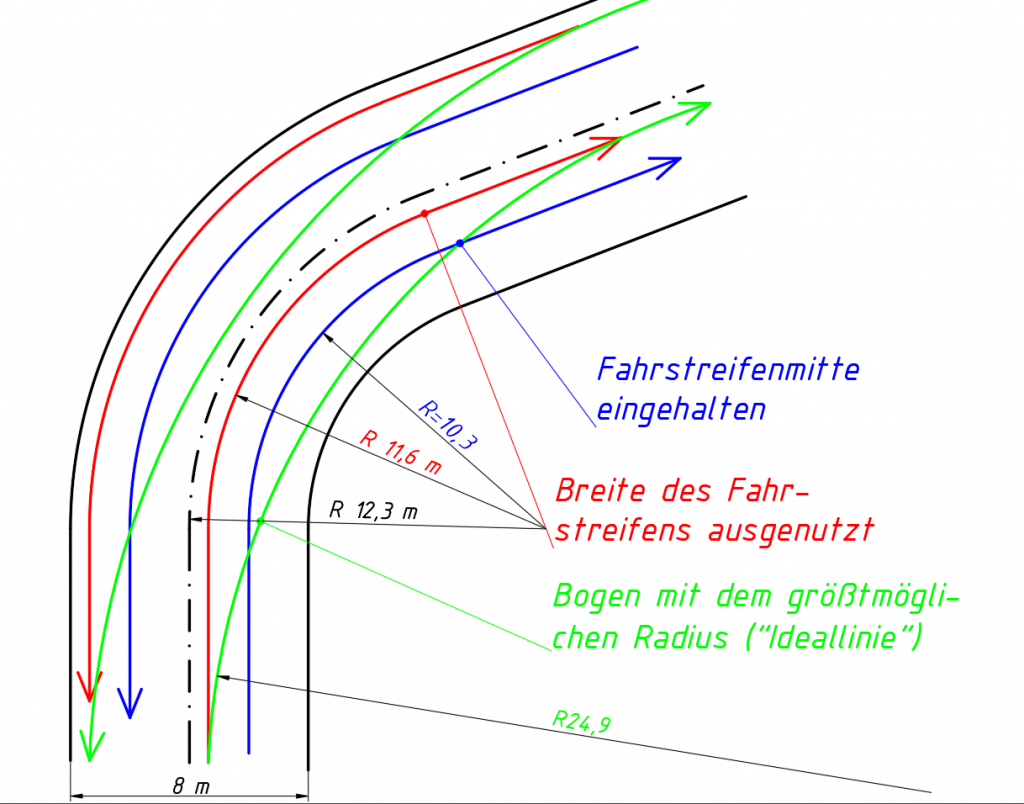
Um einen größeren Radius zu bekommen, könnte man nun die Breite des Fahrstreifens besser ausnutzen und näher an der Mittellinie fahren. Mit einem Sicherheitsabstand zu dieser von, sagen wir mal, 70 cm kämen wir dann auf einen Radius von 11,6 m. Ehrlich gesagt: Da ist nicht viel gewonnen.

Nun aber kommt der Trick: Wir fahren die Kurve in der Nähe der Mittellinie, also an der Außenseite unseres Fahrstreifens an und fahren einen Radius, der uns im Scheitelpunkt der Kurve an die Innenseite und zum Ausgang hin wieder an die Außenseite bringt. Das ist die berühmte Ideallinie – der Bogen mit dem größtmöglichen Radius. Natürlich auch wieder mit einem gewissen Sicherheitsabstand zur Außen- und Innenseite. Vor allem ist in der Linkskurve der Sicherheitsabstand im Scheitelpunkt der Kurve besonders wichtig, da wir hier durch unsere Schräglage in den Gegenverkehr hinein hängen können, auch wenn die Räder noch auf unserer Seite der Fahrbahn sind. Auch in der Rechtskurve sollten wir ihnen aufpassen, damit wir nicht etwa auf einen losen Fahrbahnrand geraten.

Aber auch mit Sicherheitsabstand wird der mögliche Radius in der Kurve ungleich größer: In unserem Beispiel sind das jetzt fast 25 m im Gegensatz zu den etwas mehr als 10 m, die wir haben, wenn wir in der Fahrbahnmitte fahren.

Und das ist jetzt das berühmte Anschneiden der Kurve, das Fahren auf der Ideallinie. Man könnte nun natürlich auf die Idee kommen, dafür nicht nur die Breite der eigenen Fahrbahnseite, sondern gleich die der kompletten Fahrbahn zu nutzen. Physikalisch geht das natürlich und wäre aus dieser Sicht noch besser, weil wir einen noch größeren Kurvenradius hinbekommen und noch schneller um die Ecke biegen können. Aber: Die Straßenverkehrsordnung verbietet dies strengstens, es gilt nämlich das Rechtsfahrgebot. Das Missachten desselben kann teuer werden, irgendwo habe ich heute etwas von 80 € Bußgeld und einem Punkt in Flensburg gelesen.

Auf der Ideallinie: Die praktische Durchführung

Großen Droh-Zeigefinger wieder eingeklappt und zurück zu unserem Merkspruch über das Gucken beim Fahren, also der so genannten Blickführung. Wir riden ja laut dem Merksprüchlein dorthin, wo wir hin looken. Also looken… äh, schauen wir beim Einfahren in die Kurve zur Mitte dieser Kurve, zu dem Punkt, wo wir im Scheitelpunkt der Ideallinie dem inneren Rand der Kurve am nächsten sind. Beim Ausfahren aus der Kurve schauen wir auf deren Ende. Und das Gas? Vor der Kurve nehmen wir es weg und wenn wir durch den Scheitelpunkt sind, drehen wir wieder auf. Und damit haben wir dann bei einer kurvigen Straße meist schon wieder den Anfang der nächsten Kurve im Blick. Auf diese Weise können wir weiche und schwingende Kurvenkombinationen hinkriegen.

Von nichts kommt bekanntlich nichts und zwischen den Endpunkten zweier gerader Linien ist nur ein einziger Radius mit tangentialen Übergängen möglich. Das gilt sinngemäß auch wenn es sich in der Praxis auch nicht um einen starren Radius, sondern um kreisbögen mit Klothoiden handelt. Mit reinen Kreisbögen kann man sich das leichter klarmachen. Ok, und musste ich mich beim Zeichnen weniger rumärgern.

Also, egal ob Kreisbogen oder Klothoiden und Kreisbogen, wenn der Radius zwischen den geraden Linien größer werden soll, müssen sie weiter auseinander sein. Und das bedeutet – man sieht das ja auch in der Abbildung – dass man die Kurve früher einleiten muss und später wieder herauskommt als wenn man einfach auf der Mitte des Fahrstreifens um die Ecke fährt.

Ein zusätzlicher Vorteil des Anfahrens einer Kurve an der Außenseite: Man sieht weiter in die Kurve hinein, was ja an sich schon ein Vorteil ist, es uns aber zusätzlich ermöglicht, den Punkt, auf den wir jeweils schauen – where you look is where you ride – ein Stück weiter nach vorne zu verlegen.

Uff! Ein Haufen Theorie auf einmal. Am besten: Ausprobieren! Vielleicht zuerst mal langsam auf dem sonntäglichen Supermarktparkplatz? Viel Spaß und Erfolg dabei und Gute Fahrt!